结构化编程简述

结构化编程来源于 20 世纪 60 年代的软件危机。那时，goto（无条件转移）语句的滥用导致了软件代码难以维护，进而让软件开发变得异常困难。有一个最有名的例子就是 IBM 为其大型机 IBM System/360 编写的系统 IBM OS/360，动用 1000 多名程序员，其开发经历了十年。

科拉多·伯姆（Corrado Böhm）及朱塞佩·贾可皮尼（Giuseppe Jacopini）于 1966 年 5 月在《Communications of the ACM》期刊发表论文，说明任何一个有 goto 指令的程序，可以改为完全不使用 goto 指令的程序。后来艾兹赫尔·戴克斯特拉（Edsger Wybe Dijkstra）在 1968 年也提出著名的论文《GOTO 陈述有害论》（Go To Statement Considered Harmful），因此结构化编程开始盛行。

结构化编程是一种编程典范。它采用子程序、代码区块、for 循环以及 while 循环等结构，来取代传统的 goto。希望借此来改善计算机程序的明晰性、质量以及开发时间，并且避免写出面条式代码。它的提出使程序设计可遵循着一定的结构形式和方法，因而提高了程序设计的效率和质量，为调试和维护程序提供了方便，以便于软件的扩充、改进、组织和管理，因此大大地降低了软件的成本。

结构化程序的特点

• 仅有一个入口
• 仅有一个出口
• 结构中任一部分都应有执行到的机会
• 不出现死循环（无休无止的循环）

结构化编程的三种基本逻辑结构

对逻辑结构进行规范，有助于算法和程序的分块、理解和编制。

以下结构中，某一块可以以除终端框外的任意块或者结构代替。结构可嵌套。

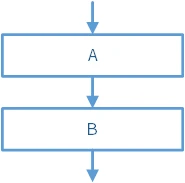
顺序结构

顾名思义，就是各个块之间按顺序执行。如图：先执行 ，再执行 ，再执行后续操作。

条件结构

条件结构是首先对变量等某一信息进行判断，根据判断的结果执行后续的流程。一般来说有两种情况：

1. 如图：如果 条件为真，执行 ，再进行后续操作；否则直接进行后续操作。

绝大多数编程语言都采用上面的做法，而非将“是”和“否”置换过来的做法。如果需要“如果 条件为真，直接进行后续操作；否则，执行 ，再进行后续操作”，最常用的做法是改变 条件为非 （）。这种情况也适用于后面的情形。

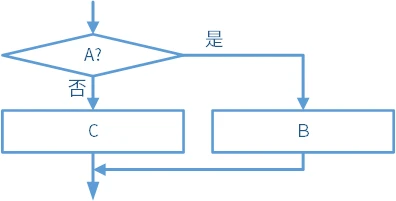
2. 如图：如果 条件为真，执行 ，再进行后续操作；否则，执行 ，再进行后续操作。

循环结构

循环结构是进行循环操作的语句。一般来说有两种情况：

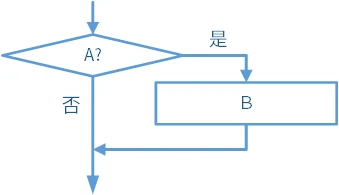
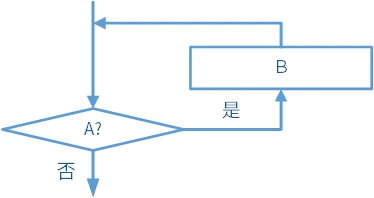
1. 直到型：先执行后判断。如图：执行 ，判断 条件是否成立。如果成立，执行 ；否则，进行后续操作。

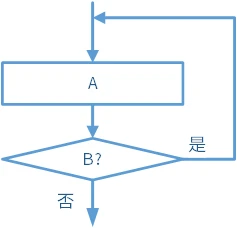
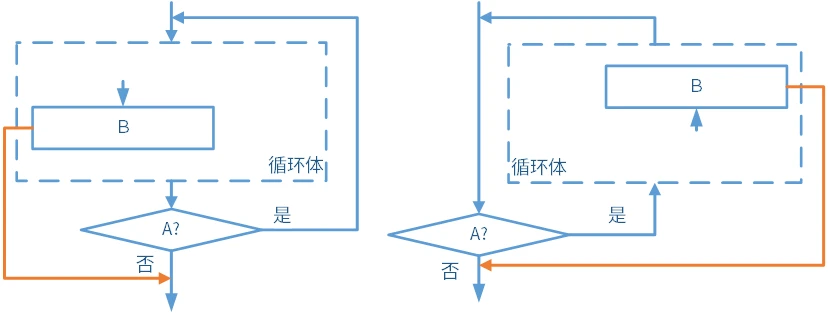
2. 当型：先判断后执行。如图：判断 条件是否成立。如果成立，执行 ，再判断 条件是否成立；否则，进行后续操作。

特殊的逻辑结构

上面的逻辑结构已经能够解决几乎所有的算法问题。不过，有一些特殊的形式，由于编程语言的支持，需要注意。

有条件跳转

之前说过，结构化编程是为了避免 goto 的滥用导致的一系列问题。虽然 goto 语句目前仍然可以在许多编程语言中使用，但是如果不是万不得已，绝对不要用。不过，事实上存在 goto 的替代品，只能作用于一个结构内。它们是 break 和 continue 语句。

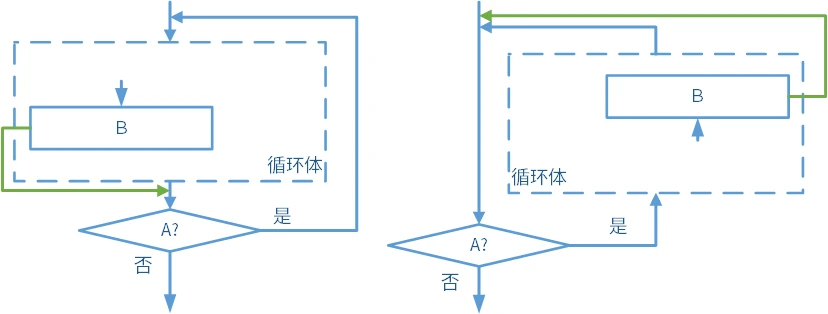
break 语句会中止循环，直接进行后续操作，如图：如果 后接 break 语句（橙色箭头），则会在执行 之后直接进行后续操作。

continue 语句会结束本轮循环，提前开始下一步循环，如图：如果 后接 continue 语句（绿色箭头），则会在执行 之后，跳转至循环判断语句。

它们常常与条件结构共用。

switch 结构

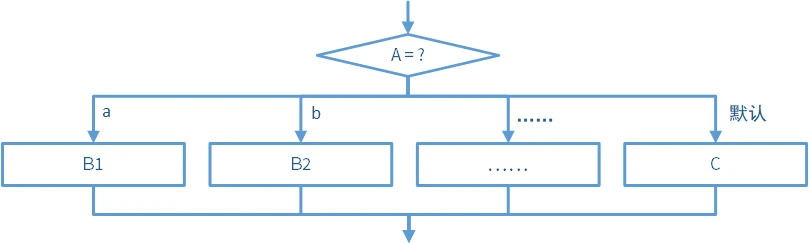
上面的条件结构只支持是/否的二分支情况。在表达多分支的条件结构时，我们使用 switch 结构。

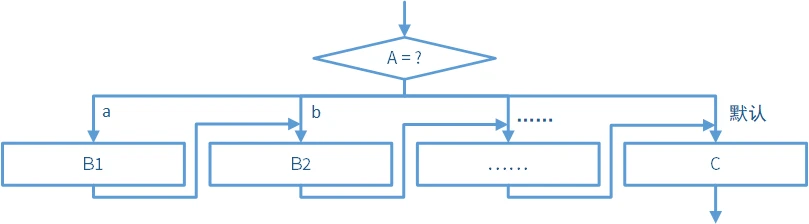
switch 结构的流程图如下：先判断 的值，当 时，执行 ，再执行 ，执行到 ，然后进行后续操作；当 时，执行 ，执行到 ，然后进行后续操作；……若无对应值，执行 ，然后进行后续操作。

这样的结构当然不能符合要求。在实际应用中，我们通常使用 break 语句来让分支执行完毕后直接进行后续操作。下图是当所有分支都使用 break 语句之后的流程图：先判断 的值，当 时，执行 ；当 时，执行 ；……若无对应值，执行 。再执行后续操作。

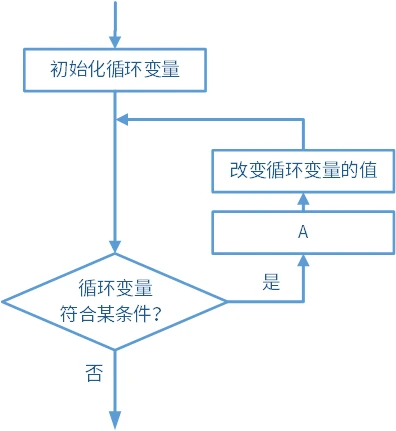
for 循环

for 循环是一种特殊的当型循环结构。它是先初始化某个循环变量，然后判断循环变量是否符合某条件。如果符合，执行 ，再改变循环变量的值，再判断循环变量是否符合某条件。否则，执行后续操作。

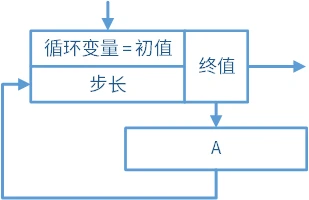
在 20 世纪 80 年代的江苏科学技术出版社出版的《广播电视中专教材 计算机应用基础》中，for 循环在流程图中有一种简写符号，这种简写符号适用于上图中执行 之后对循环变量进行加操作的情况。但是现在应该是很少用了：

递归

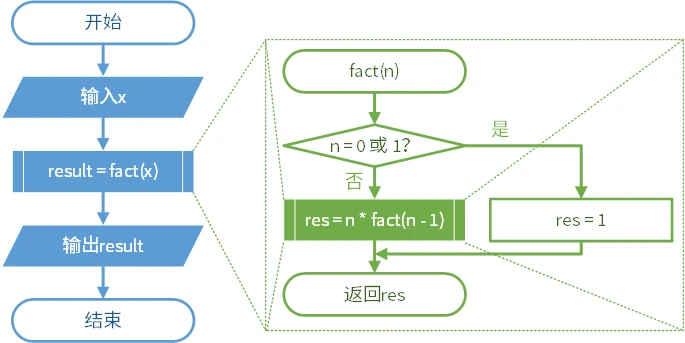
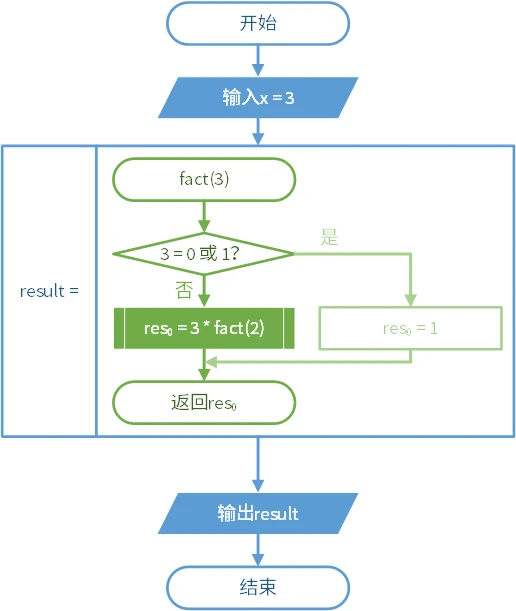
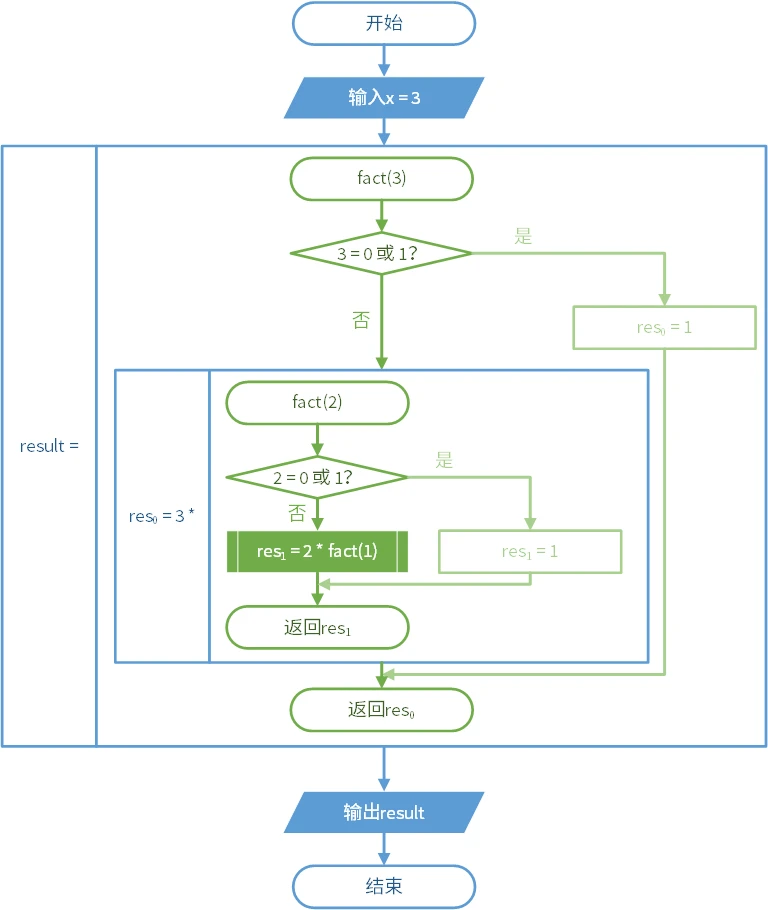
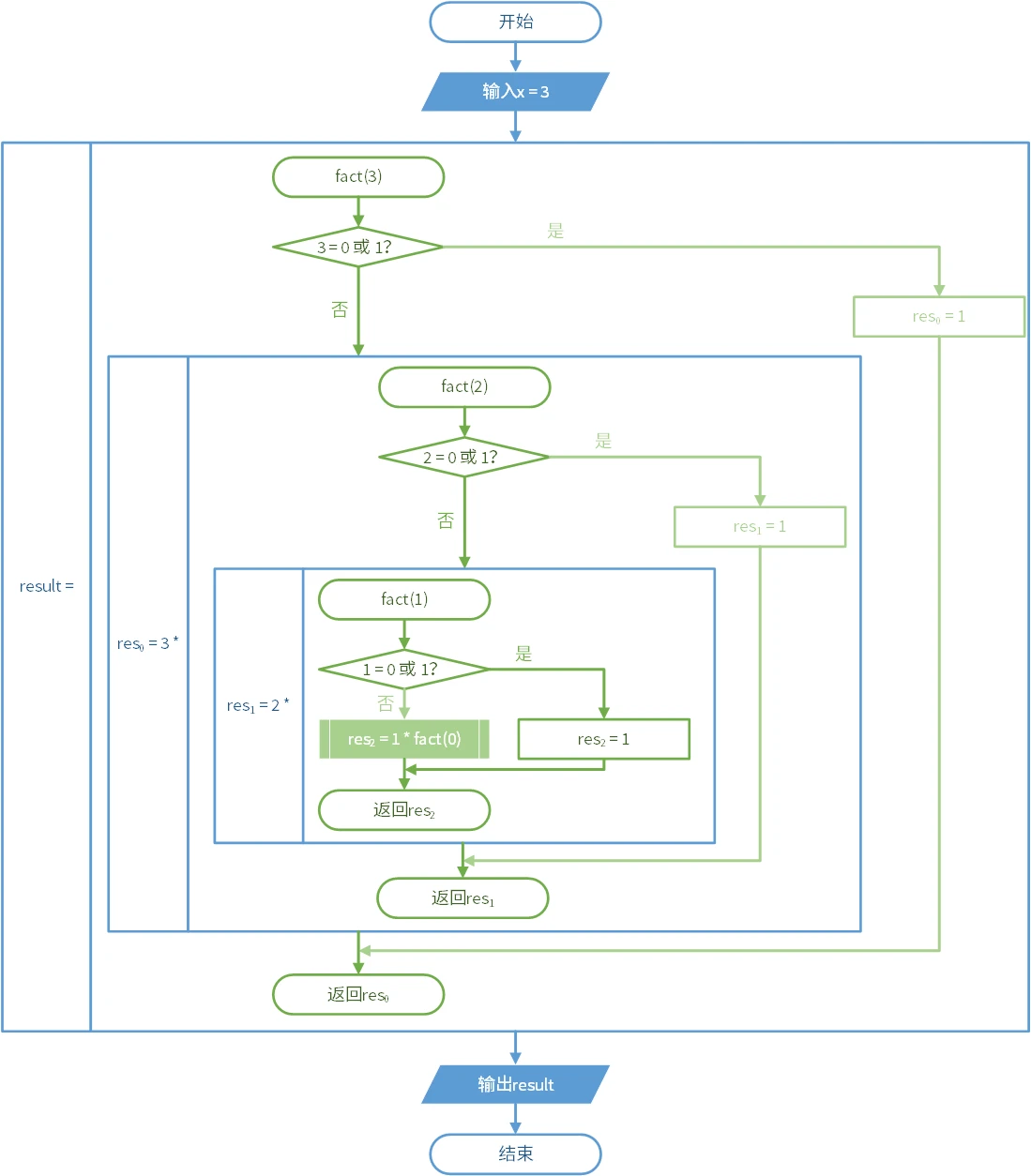
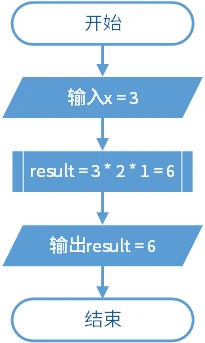
递归是子程序中调用本身的情况。这种情况难以使用流程图描述。它常常与条件结构共用。以下的图是一个求阶乘的递归算法。

在这里，递归的复杂程度取决于输入的 。当输入 时，递归过程如下：

参考资料

• 结构化编程 - 维基百科，自由的百科全书
• 广播电视中专教材 计算机应用基础。江苏科学技术出版社