简介

两个或多个正整数数的公约数是，对于这些数，存在一个正整数，可以整除它们。公约数可能有若干个，而其中最大的就是最大公约数。

也就是：

即为 中各数的最大公约数。

从人类的做法推导

我们计算最大公约数的时候，通常用短除法来计算。具体的方法是：同时让这些数除以一个比较小的公约数，得到的结果再这样操作，直到找不到大于等于 2 的公约数；将除数相乘即得到最大公约数。比如：

通过经验，人是可以快速找到一些较小的公约数，写在除数上的。但是，计算机却无法这么做。但是计算机可以从 1 开始，判断某个整数是否能整除所有给定的数。如果能，即为公约数，记下来；否则，除数加 1，再试。

但是，算法是有限的，到什么时候停止呢？根据常理，一组数的最大公约数一定不大于这组数的最小的数。因此，如果算到这组数的最小值的话，就不用再算下去了。

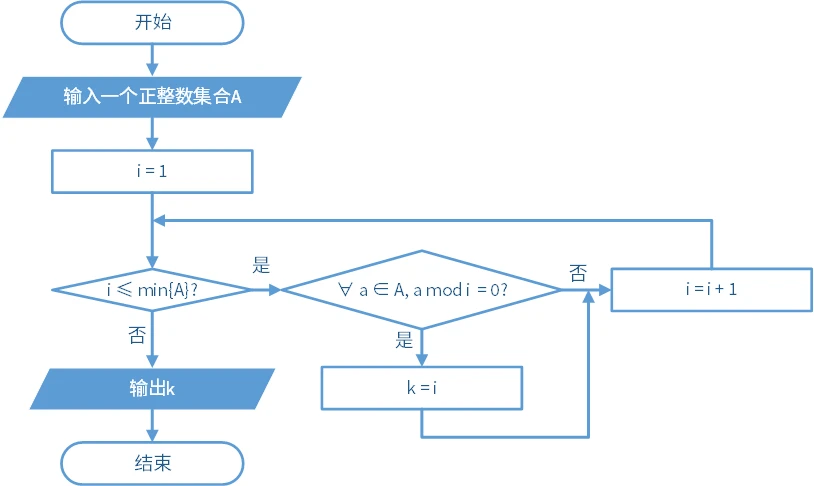
由此可以推导出流程图如下：

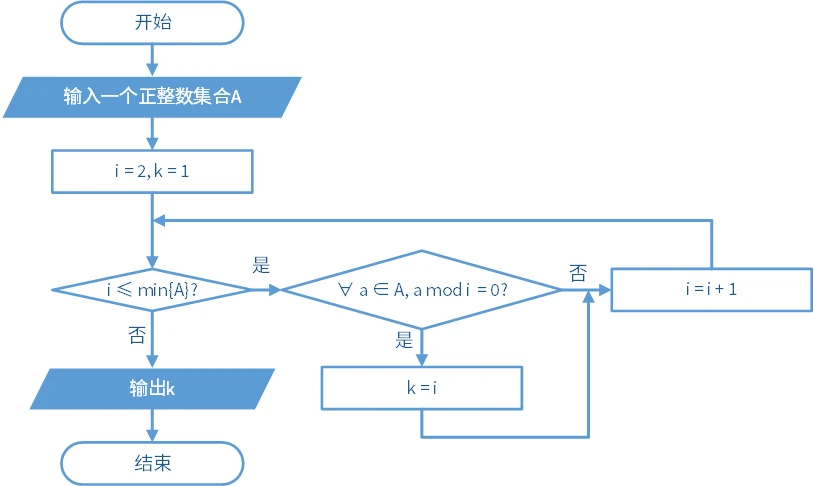
鉴于 1 能够整除所有正整数，我们可以让循环从 2 开始。这样，流程图如下：

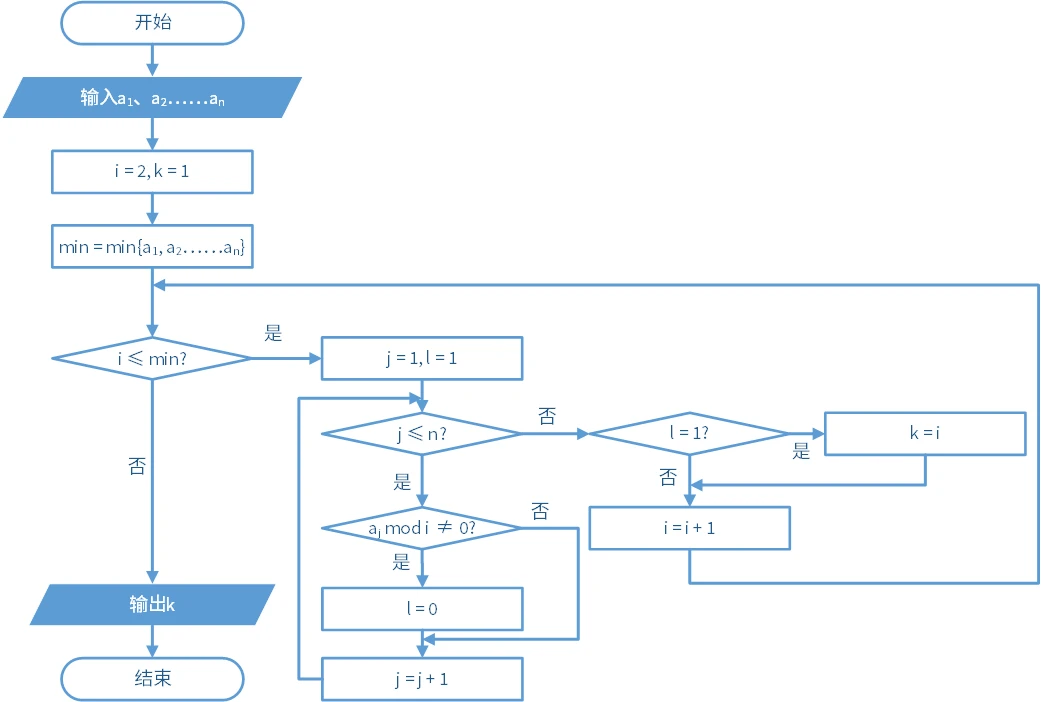
如果我们把“”的判断展开，则如下：

已经非常复杂了。

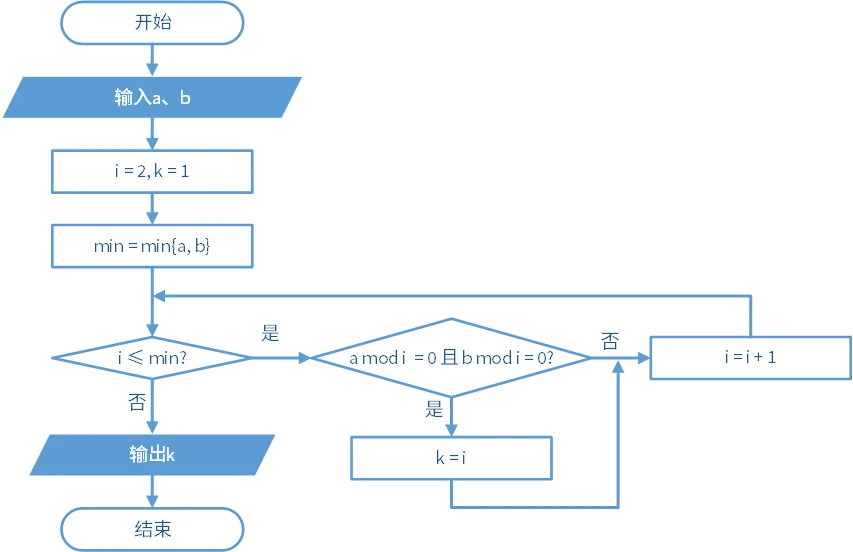
实际应用中，我们更多的是计算两个数之间的最大公约数。这样，流程图可以简化如下：

不过这个方法在计算的时候，如果是小的数字还可以，遇到大数的时候，计算时间就非常长。

这时候还可以使用更加简便的算法。

辗转相除法

辗转相除法又称欧几里得算法，首次出现于《几何原本》中，被人们认为是史上第一个算法。它可以用于求两数的最大公约数。

首先，用两数中较大数除以较小数，求得数；再用较小数和余数按上述操作进行相除；直到余数为 0。此时的除数即为最大公约数。

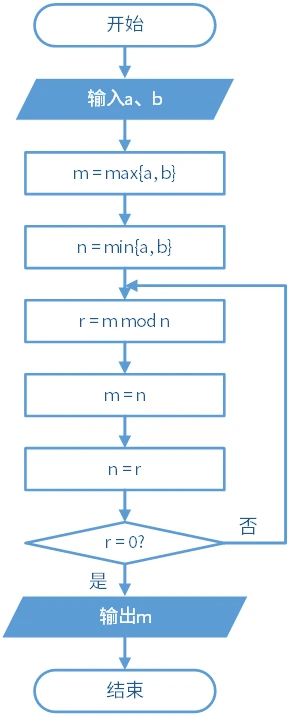
流程图表示如下：

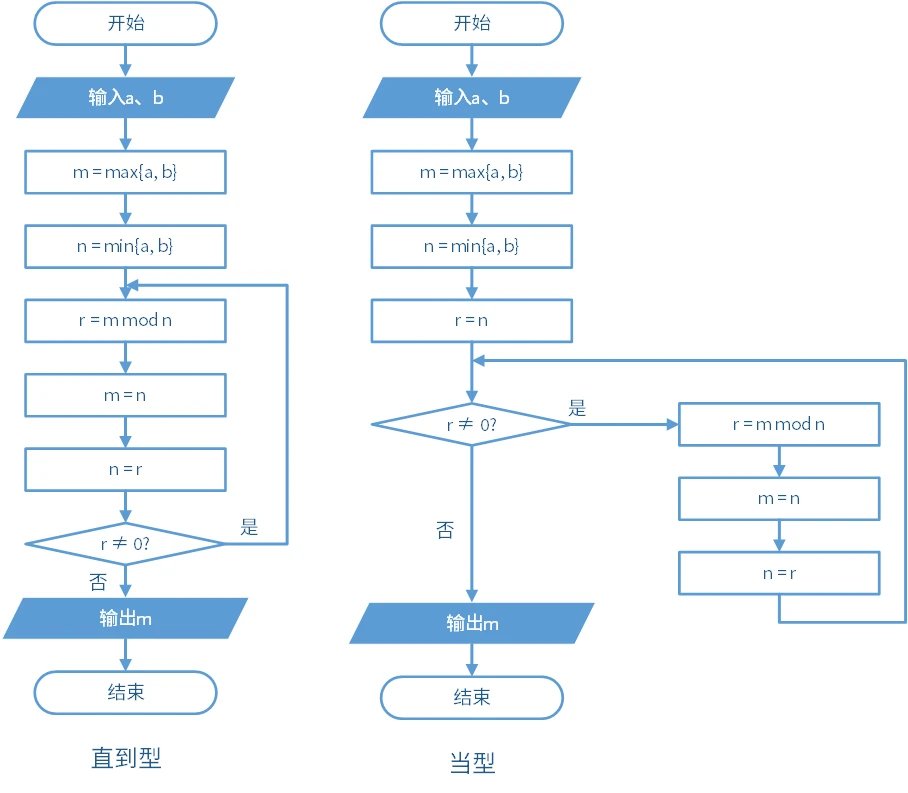
考虑到许多编程语言使用的是 DO-WHILE 型的直到型循环结构，还有一些语言没有直到型循环结构，流程图改写为如下：

其中当型的流程图在循环结构前有一个定义变量 的操作。这里的 的赋值只要不等于 0 就可以了。

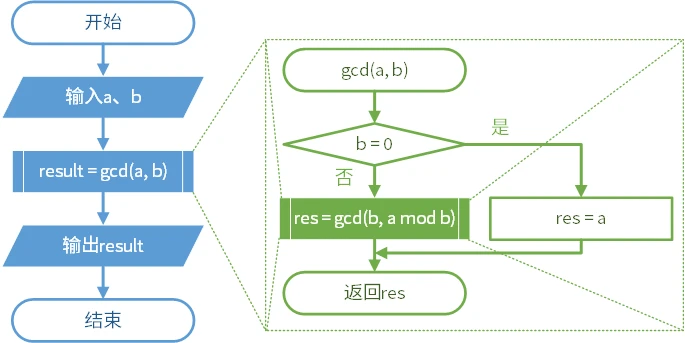
此外，还有递归型的流程图：

更相减损术

更相减损术是《九章算术》中给出的求两个数的最大公约数的方法：

可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。

算法描述为：

第一步：任意给两个正整数；判断它们是否都是偶数，如果是，用 2 约简，并记下次数；否则，进行下一步；

第二步：以较大的数减去较小的数，把差与较小的数相比，并用大数减小数。继续此操作，使所得数相等为止。记下这个数。

第三步：**如果第一步有约简，第二步所得的数乘上 2 乘约简次数就是最大公约数。否则，**第二步所得的数就是最大公约数。

（人教版的教科书上对这个的解释有问题……粗体字表示增加的内容）

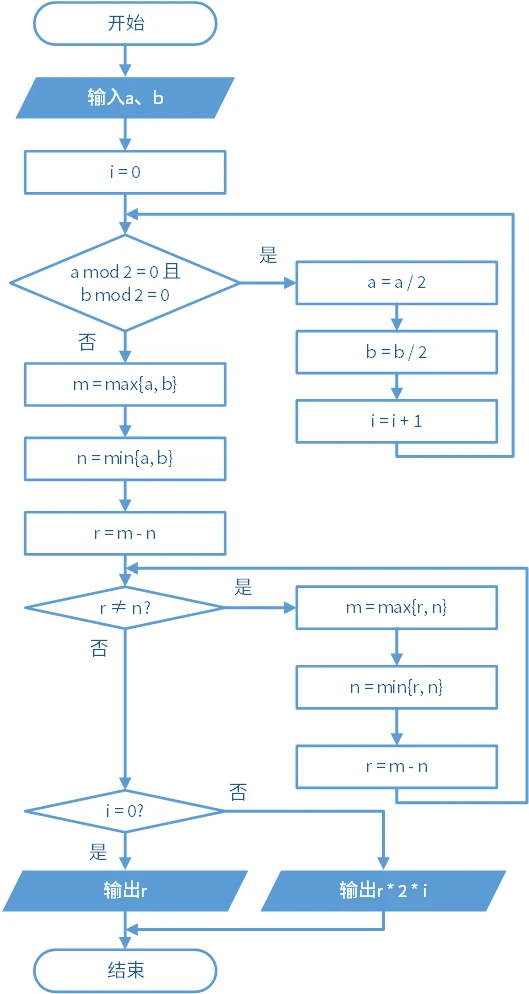
流程图如下：

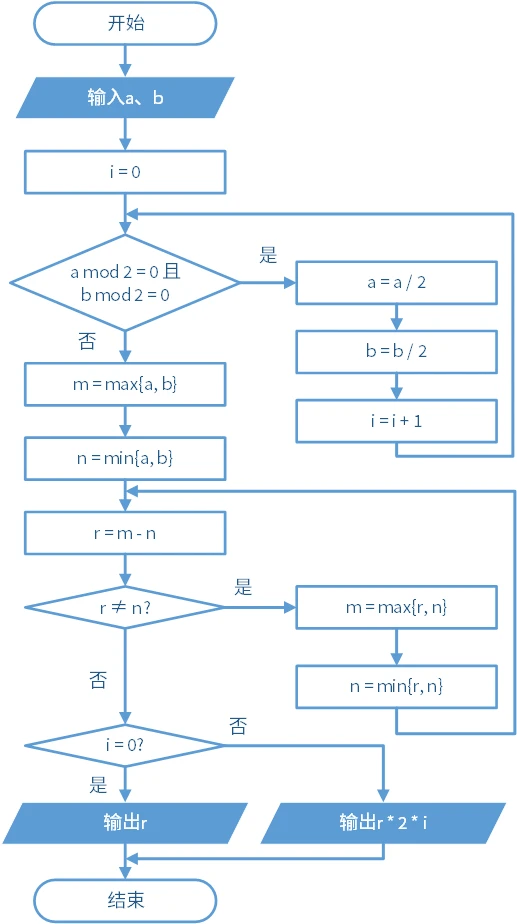
标准化后如下：

看起来非常麻烦。

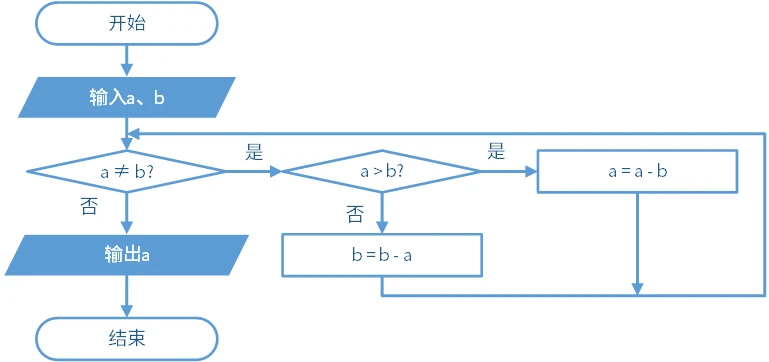
不过，还有一个简单的算法：

实际上这和辗转相除法很相似了。在维基百科上，它们是在一个词条内的，而且上面的算法被称为欧几里得算法的减法形式。

三者的比较

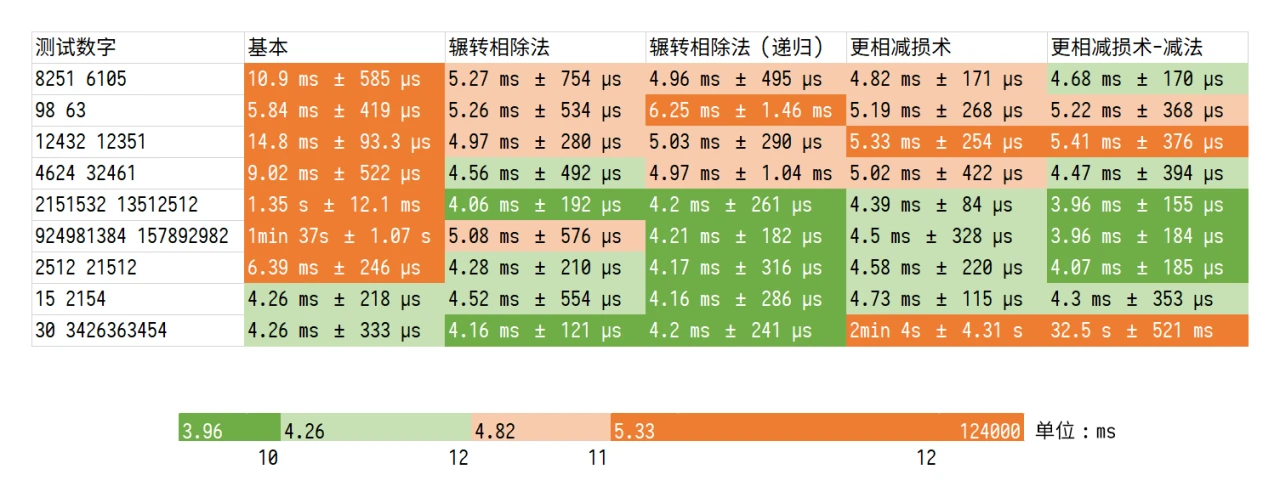
在现代，算法之间的比较主要体现在效率上。在下面，我将使用 IPython 的工具来测试它们的运行速度（使用语言为 Python，在安装 Windows 10 专业版和 Python 3.6 的华硕 N551ZU 上进行，结果仅供参考）。

演示视频

从这里就能看出来，虽然现在电脑硬件水平的发展相当成熟，但是各个算法之间的运行速度还是有比较明显的差别的。

之前的那个直接求最大公约数的方法，运算速度相对于其他的算法都比较慢，尤其是在两个数都非常大的情况下。相比之下，其他算法的运算速度和它的运算速度相差悬殊。

另外，更相减损术在两数相差悬殊的时候，运算速度也会减慢。

从这里我们可以看出优化算法的意义——可以显著减少运行时间，提高效率，节能。这个测试还是在比较好的机器上进行的，如果是在简单的单片机上，差别就更加明显了。

参考资料

如果大家想了解关于这两个算法的更多内容，也可以看看。

• 辗转相除法 - 维基百科，自由的百科全书
• 普通高中课程标准实验教科书（必修） 数学（A 版） 必修 3. 人民教育出版社
• 辗转相除法、更相减损法、Stein 算法 - CSDN 博客